Voici une sélection de deux problèmes d’olympiades (orales !) soumis aux élèves moscovites de 6ème année (2ème année du secondaire) en février 2011.
Le premier est intéressant pour les développements et commentaires qu’il appelle, le second est, par la solution proposée, un modèle d’élégance et de concision.
Les deux problèmes sont des créations de A.V.Shapovalov .
Le dragon et les bonnets
Enoncé
Un dragon a enfermé dans une caverne six nains et leur dit : « J’ai sept bonnets de couleurs différentes aux couleurs de l’arc en ciel. Demain matin, je vous banderai les yeux, je vous mettrai à chacun un bonnet et je cacherai le septième bonnet. Ensuite, je vous enlèverai le bandeau des yeux et vous pourrez voir le bonnet sur la tête des autres mais je ne vous autoriserai pas à communiquer entre vous. Ensuite chacun, en cachette des autres, me dira la couleur du bonnet caché. Si trois au moins d’entre vous devine cette couleur, je vous libérerai tous, sinon vous constituerez mon repas. »
Comment les nains doivent-ils s’entendre à l’avance pour être sauvés ?
Solution
Chaque nain voit tous les bonnets sauf deux : le sien et celui qui est caché. Il s’agit de se mettre d’accord sur la couleur à choisir parmi celles de ces deux bonnets. Ceci peut se faire, par exemple, de la manière suivante :
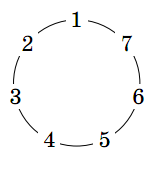
Numérotons les couleurs de 1 à 7 (par exemple, dans l’ordre des couleurs de l’arc en ciel) et disposons les en cercle.
Considérons l’arc de cercle, orienté dans le sens des aiguilles d’une montre, le plus court entre les deux couleurs (ou les numéros les représentant). La stratégie est de choisir la couleur correspondant à l’origine de cet arc.
Dans ce cas, trois nains fourniront la bonne réponse et trois se tromperont. Si par exemple, le chapeau caché est le chapeau de couleur 1, alors les nains ayant les bonnets de couleurs 2, 3 et 4 devineront la couleur du bonnet caché.
On peut aussi agir autrement. Si les deux couleurs que ne voit pas un nain sont représentées par des couleurs de même parité, il proposera la couleur associée au plus grand des deux nombres, dans le cas contraire, il choisira la couleur associée au plus petit des deux nombres. Quelle que soit la couleur du bonnet caché, trois nains la proposeront. Par exemple, si le bonnet de couleur 3 est caché, les nains ayant les bonnets de couleurs 1, 4 et 6 devineront correctement la couleur du bonnet caché. Les autres cas peuvent être traités manière analogue.
Commentaires
-
Le principe de décision (la stratégie) des nains, exposé dans la seconde solution, est utilisée dans les tournois d’échecs à un nombre impair de participants pour que chaque joueur joue Noir et Blanc un nombre égal de parties. Plus précisément, chaque participant au tournoi reçoit son numéro et si deux joueurs ayant des numéros de même parité s’affrontent, celui qui a le plus grand numéro joue Blanc sinon c’est celui qui a le plus petit numéro qui joue Blanc. On peut se convaincre que chaque joueur joue alors Blanc et Noir le même nombre de parties.
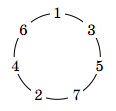
- A strictement parler, la seconde solution ne se distingue de la première que par la manière de numéroter les couleurs. Si on dispose les couleurs sur le cercle comme dans la figure précédente, la stratégie des nains de la première solution, décrit exactement la seconde.
- On peut démontrer qu’aucun accord ne permettra que, à coup sûr, plus de la moitié des nains découvrira la couleur du bonnet caché [1].
Un cube coupé en huit
Enoncé
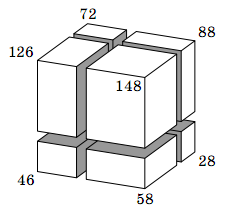
Un cube en bois est scié en trois coups de scie parallèlement aux faces comme indiqué dans la figure ci-dessous. Sur cette figure, sont aussi mentionnées les aires des surfaces de sept des huit petits cubes obtenus.
Quelle est l’aire de la surface du cube invisible ?
Solution
Sur chaque petit cube, la surface des coups de scie correspond à la moitié de la surface totale. Nous ne considérerons que l’aire des coups de scie. Colorions les petits cube en noir et en blanc comme dans la figure ci-dessous.
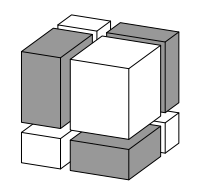
De la sorte, toutes les paires de faces isométriques adjacentes sont de couleurs différentes. Pour cette raison, la somme des aires « noires » des coups de scie est égale à la somme des aires « blanches » des coups de scie. De là, la somme des aires des surfaces des cubes noirs est égale à la somme des aires des surfaces des cubes blancs.
Si ![]() est l’aire de la surface du cube caché, on a l’équation
est l’aire de la surface du cube caché, on a l’équation
![]()
Alexandre Vasilievich Shapovalov est connu pour ses recherches dans le domaine de la construction et de la résolution de problèmes. Dans sa brochure "Le principe des places étroites" (disponible ici en Russe...), il propose de s’intéresser aux voies étroites par lesquelles on passe en résolvant un problème. Ces endroits sont parfois ceux où on peut le plus facilement trouver une contradiction ou établir plus facilement une étape vers la construction de la solution.
L’Urem vous en dira plus, lorsqu’elle aura décortiqué ce texte.
Documents joints
 Document, PDF, 140.5 ko
Document, PDF, 140.5 ko
Notes
[1] Bien sûr, si chaque nain choisit au hasard entre les deux couleurs, il est possible que plus de la moitié des nains citent la bonne
- Podcast et RSS
- Plan
- Contact
- Mentions
- Aide
- Rédaction
- Se connecter

-
2006-2024 © UREM-ULB :
Unité de Recherche sur l’Enseignement des Mathématiques - Tous droits réservésCe site est géré sous SPIP 3.2.8 et utilise le squelette EVA-Web 4.2

Dernière mise à jour : mercredi 14 avril 2021

