Le magazine populaire et scientifique soviétique, Kvant (Quantum en Anglais) consacré essentiellement aux mathématiques et à la physique, et destiné aux élèves et étudiants fut crée en 1970 à l’initiative de l’académicien Piotr Kapitsa. Jusqu’en 1990, il était tiré à plus de 250000 exemplaires... A.Kolmogorov en était un des rédacteurs et Issac Kikoïn en était le rédacteur en chef.
Des temps difficiles
En 1985, l’Unesco déclarait que Kvant était un journal unique en son genre. Malgré cette reconnaissance, le tirage tomba au cours des années 90 à quelques milliers d’exemplaires. L’Etat Russe (et non plus soviétique) n’apporta plus son soutien à l’initiative : se posèrent des problèmes de locaux, d’équipe vieillissante, etc.
Pendant 12 ans, jusqu’en juillet 2001, Kvant connut, sous le nom de Quantum, une traduction en Anglais. La "National Science Teachers Association" (NSTA) soutenait le projet avec enthousiasme mais dut arrêter la publication, assurée par Springer, suite à de nombreuses difficultés financières.
Les difficultés ne s’arrêtèrent pas là ! A Moscou, des problèmes juridiques s’ajoutèrent au problèmes financiers ; le problème étant de savoir qui aurait le droit de reprendre les activités. L’affaire n’est, semble-t-il, pas close à ce jour.
Vers un renouveau ?
Fort heureusement, le Centre de Moscou pour la Formation Continue (Мцнио) [1] s’est lancé dans le projet d’une archive électronique de Kvant. L’ensemble est déjà assez complet même si la qualité des documents scannés [2], comme le reconnaît le centre, laisse parfois à désirer.
On trouvera sur le site de la NTSA un exemplaire en anglais de Quantum. L’AMS propose aussi trois recueils (payants !) d’articles de Quantum repris sous les thèmes Algèbre, Analyse et Combinatoire. La page wikipedia russe consacrée à Kvant évoque sans autre précision deux recueils d’articles qui auraient été publiés en Français.
Ceux que la pratique de la langue de Pouchkine rebute, pourront toujours se contenter des couvertures de Kvant de 1970 à 1996.
Au delà de l’archivage, le Centre a proposé la création du clone Kvant+ de Kvant. Là encore, les soucis juridiques devaient ralentir cette louable tentative de renouveau. Le feuilleton, n’est pas terminé. Mais, ne perdons pas espoir : en 2002, Kvant n’annonçait-il pas fièrement son cent millième anniversaire ... en base 2 (premier numéro en 1970). Il faut rester optimiste.
Le grand martyr Pétia [3]
Voici enfin la traduction d’un petit article, simple, paru dans Kvant n°6 de 2002. Il permet d’apprécier l’esprit dans lequel de nombreux articles étaient rédigés : bien souvent dans l’optique de l’analyse et de la résolution de problèmes. L’article est signé I.Akoulitch.
Considérons les nombres positifs ![]() et
et ![]() .
.
Il est bien connu que leur moyenne arithmétique est ![]() et leur moyenne géométrique
et leur moyenne géométrique ![]() . Un peu moins connue est leur moyenne harmonique
. Un peu moins connue est leur moyenne harmonique ![]() .
.
Il est clair que ![]()
C’est à dire que le produit de la moyenne arithmétique et de la moyenne harmonique est égal au produit des deux nombres ![]() et
et ![]() .
.
En 1999, A.Kanell comprit que de ce simple fait, on pouvait "façonner" un bon problème d’olympiades, par exemple de la façon suivante :
Soit ![]() ,
, ![]() et, pour un entier naturel quelconque
et, pour un entier naturel quelconque ![]() ,
, ![]() et
et ![]() les moyennes arithmétiques et harmoniques respectives des nombres
les moyennes arithmétiques et harmoniques respectives des nombres ![]() et
et ![]() . Trouver le produit
. Trouver le produit ![]() .
.
La solution consiste en ce que le produit ![]() est le même pour tout
est le même pour tout ![]() et que donc
et que donc ![]() .
.
Mais l’auteur, apparemment, décida que l’énoncé paraissait un tantinet ennuyeux et le rendit plus vivant de la manière suivante :
Sur le tableau d’un laboratoire, sont écrits deux nombres. Chaque jour, le vieux collaborateur scientifique Pétia (Pierre) efface du tableau les deux nombres et écrit à la place leur moyenne arithmétique et leur moyenne harmonique. Le matin du premier jour, sur le tableau sont écrits les nombres ![]() et
et ![]() . Trouver le produit des nombres que Pétia écrira le soir du 1999ème jour.
. Trouver le produit des nombres que Pétia écrira le soir du 1999ème jour.
C’est sous cette forme que le problème fut présenté aux élèves de 9ème [4] à la LXIIème Olympiade de Moscou. Apparemment, le problème ne se distingue du problème original que par le contexte. Par essence les deux problèmes semblent équivalents. Mais examinons de plus près l’action de notre vieux collaborateur scientifique...
Le premier jour, il écrit au tableau les nombres ![]() et
et ![]() .
.
Le second jour, il écrit ![]() et
et 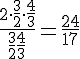
D’ailleurs, pourquoi calculons-nous la moyenne harmonique ? Vous vous rappelez que le produit des moyennes arithmétiques et géométriques est constant et égal à 2. De sorte qu’on peut ne calculer que la moyenne arithmétique.
Le troisième jour (vérifiez si vous doutez [5]), sur le tableau apparaissent les nombres ![]() et
et ![]() , le quatrième
, le quatrième ![]() et
et ![]() , le cinquième
, le cinquième ![]() et
et ![]() .
.
Le sixième jour, Pétia écrit : ![]() et
et ![]()
Au delà, les choses se compliquent ...
Pétia, bien sûr, peut utiliser un ordinateur, il est un vieux collaborateur scientifique, après tout. Mais il est intéressant de savoir si Pétia pourra écrire les nombres sur le tableau, c’est à dire, aura-t-il suffisamment de place ? Et un ordinateur pourra-t-il calculer ces nombres ? Ils croissent tellement rapidement [6]...
Le lecteur, sans doute, pressent déjà la réponse. Mais s’en convaincre ne doit gêner personne.
Écrivons le nombre ![]() sous forme d’une fraction irréductible
sous forme d’une fraction irréductible ![]()
Alors
![]() ,
,
![]() ,
,
![]() .
.
De sorte que ![]() . Remarquez que la majoration est assez grossière (par induction, on peut prouver que
. Remarquez que la majoration est assez grossière (par induction, on peut prouver que ![]() de sorte qu ’en fait :
de sorte qu ’en fait : ![]() [7].
[7].
Nous savons déjà que ![]() . Ce qui implique que :
. Ce qui implique que :
![]()
Du fait que ![]() , on a :
, on a :
![]()
Ce qui signifie que les termes de la fraction que Pétia doit écrire sur le tableau au 1999ème compteront plus de ![]() chiffres.
chiffres.
Dire que ce nombre est grand ne signifie rien du tout. Il est absurdement grand ! Même si Pétia ecrit un milliard de chiffres à la seconde, alors il lui faudra ![]() secondes [8]
secondes [8]
Du fait que ![]() , Pétia aura besoin de plus de
, Pétia aura besoin de plus de ![]() années pour écrire seulement un des termes d’une des deux fractions...
années pour écrire seulement un des termes d’une des deux fractions...
Notes
[1] Il y a aussi une page d’accueil en Anglais
[2] uniquement pour les numéros les plus anciens
[3] Les martyrs et les grands martyrs sont honorés dans l’Eglise Orthodoxe
[4] Elèves de 15-16 ans
[5] Proverbe russe : le doute est le commencement de la sagesse
[6] du moins les termes des fractions impliquées
[7] A ce propos et à propos de beaucoup d’autres choses, on peut lire l’article de V.Senderov et A.Spivak "L’équation de Pell" dans Kvant n°3
[8] n.d.t. :pour écrire un terme d’une des deux fractions !
- Podcast et RSS
- Plan
- Contact
- Mentions
- Aide
- Rédaction
- Se connecter

-
2006-2024 © UREM-ULB :
Unité de Recherche sur l’Enseignement des Mathématiques - Tous droits réservésCe site est géré sous SPIP 3.2.8 et utilise le squelette EVA-Web 4.2

Dernière mise à jour : mercredi 14 avril 2021

